2025-Q1-AI 2. Matricu transformācijas - Asteorid spēle - Lineārā algebra

2.1. Video / Materials

19 februāris Riga, Zunda krastmala 10, 122 + Remote

Zoom (ielaidīšu un atstāšu kā host): https://zoom.us/j/3167417956?pwd=Q2NoNWp2a3M2Y2hRSHBKZE1Wcml4Zz09

Whiteboard (ir iedotas tiesības): https://www.figma.com/board/FfmDexmoHrIXq93oS9GQhn/2025-Q1-AI-2.-Matricu-transform%C4%81cijas---Asteorid-sp%C4%93le---Line%C4%81r%C4%81-algebra?node-id=0-1&t=iFxECdcKS3ystGxI-1

Dot product: https://www.mathsisfun.com/algebra/matrix-multiplying.html

Very good materials on linear algebra and other math topics: https://www.3blue1brown.com

2.2. Matricu sakalārais reizinājums

1D piemērs

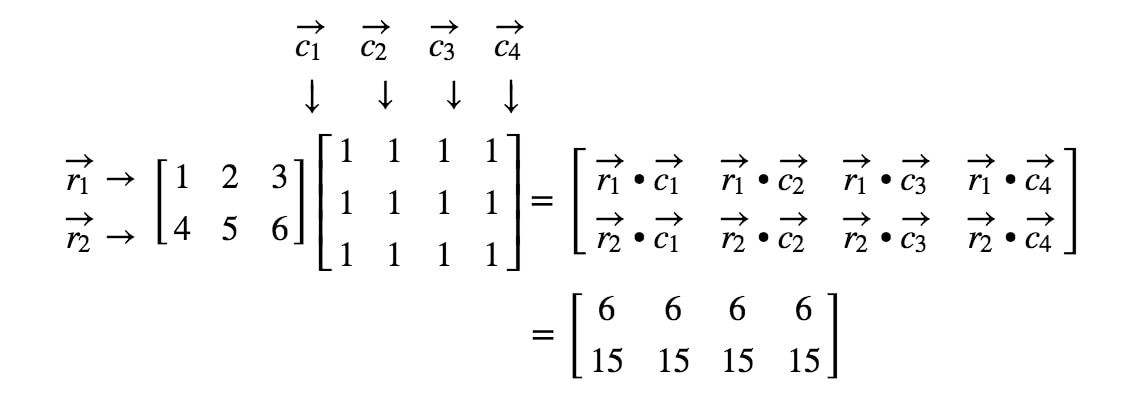
2D piemērs:

Dot product examples:

https://www.studypug.com/algebra-help/multiplying-a-matrix-by-another-matrix

Template: https://share.yellowrobot.xyz/quick/2024-9-27-FA30B918-38A3-4915-8B0C-8D155EA84C53.zip

Iesniegt kodu kā failu.

2.3. Implementēt leņķa maiņu player

Par pamatu izmantot sagatavi no 2.3. uzdevuma ar dot product implementāciju no 2.1. uzdevuma.

Izmantot pirmkoda sagatavi un sekot materiālam nodarbībā

https://share.yellowrobot.xyz/quick/2024-9-27-B1CAC014-88C1-44CF-8FAB-58F214191790.zip

Implementēt rotācijas matricu un panākt, ka kosmosa kuģītis rotē ap savu asi Implementēt leņķa maiņu ar bultiņām, izpildīt todo, iesniegt pirmkodu.

Iesniegt kodu kā failu.

2.4. Implementēt vec2d_to_vec3d un vec3d_to_vec2d

Par pamatu izmantot sagatavi no 2.3. uzdevuma ar dot product implementāciju no 2.1. uzdevuma. Pārveidot 3d vektorus uz 2d vektoriem un otrādi tikai izmantojot identitātes matricas, dot product un saskaitīšanu Iesniegt kodu kā failu un pievienot screenshot.

2.5. Implementēt translācijas matricu

Par pamatu izmantot sagatavi no 2.3. uzdevuma ar dot product implementāciju no 2.1. uzdevuma.

Implementēt translation_mat. Panākt, ka Player ir nobīdīts tā, lai rotētu ap savu asi nevis ap apakšējo līniju. Implementēt, ka objekti pārvietojas, izmantojot translation_mat. Rotāciju un Translāciju obligāti ir jāapvieno vienā kopējā matricā C!

Vienādojums:

Iesniegt kodu kā failu un pievienot screenshot.

2.6. Implementēt scaling matricu Player

Par pamatu izmantot sagatavi no 2.3. uzdevuma ar dot product implementāciju no 2.1. uzdevuma. Implementēt scaling matricu un saspiest Player, lai tas nebūtu tik plats (transformāciju iekļaut self.C matricā) Iesniegt kodu kā failu un pievienot screenshot.

2.7. Implementēt riņķa līnīju planētai

Implementēt riņķa līnīju planētai un asteroīdus ar randomization

Riņķa līnijas zīmēšanas algoritms: https://www.mathopenref.com/coordparamcircle.html

Vienādojums, izmantot delta theta 0 - 360 gradiem for loopā

2.8. Implementēt gravitācijas vienādojumu

Par pamatu izmantot sagatavi no 2.3. uzdevuma ar dot product implementāciju no 2.1. uzdevuma.

Implementēt simulētu gravitācijas vienādojumu starp planētām un spelētāju. Izmantot "game physics" versiju:

Iesniegt kodu kā failu un pievienot screenshot.

2.9. Mājasdarbs - Pabeigt spēli

Izmantojot kodu, kas iegūts tiekot līdz 2.7. implementēt sekojošās izmaiņas:

1. Implementēt Skew matricu, un izmantot to, lai nejaušā veidā saspiestu asteroidus

2. Implementēt sadursmju atpazīšanu. Piešķirt punktus par ar raķeti sašautiem asteroīdiem. Savukārt, ja spēlētājs saduras ar planētām vai asteroīdiem, tad spēle tiek zaudēta.

3. Implementēt planētas, kurām ģeometriju zīmē ar (Mid-Point Circle Drawing Algorithm). Var ģenerēt punktus pa kvadrantiem. Vienādojums: eps = 0.5 radius = 2

Saturs

Video Piemērs: https://youtube.com/live/bAGVxu-xkJ0?feature=share

Pabeigts koda piemērs: https://share.yellowrobot.xyz/quick/2025-2-12-30073936-23D3-4D89-B241-63822188BB4D.zip

1. Iziet cauri sliktajiem piemēriem no iepriekšējās nodarbības (komentāri augstāk)

2. Explain Dot product + give task https://www.studypug.com/algebra-help/multiplying-a-matrix-by-another-matrix

   ROWS must match COLUMNS

   $$\begin{array}{}\text{(2)}& \begin{array}{c}a=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right],a^T=\left[\begin{array}{ccc}1& 2& 3\end{array}\right],b=\left[\begin{array}{c}4\\ 5\\ 6\end{array}\right]\\ a+b=\left[\begin{array}{c}5\\ 7\\ 9\end{array}\right]\\ a^T\cdot b=1\cdot 4+2\cdot 5+3\cdot 6=32\\ b=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right],a=\left[\begin{array}{cccc}1& 2& 3& 4\end{array}\right]\\ b\cdot a=\left[\begin{array}{cccc}1\ast 1& 1\ast 2& 1\ast 3& 1\ast 4\\ 2\ast 1& 2\ast 2& 2\ast 3& 2\ast 4\\ 3\ast 1& 3\ast 2& 3\ast 3& 3\ast 4\end{array}\right]\end{array}\end{array}$$

    

    

xxxxxxxxxx
1
1
  1. Paskaidrot, ka pat 1D vektori ir 2D

http://hyperphysics.phy-astr.gsu.edu/hbase/vsca.html

1. 

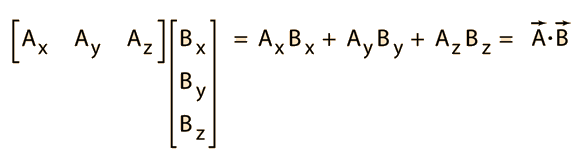
2. Matrix example

3.  

   

4. 

   

5. 

6. identity matrix (Propery, check if it is inverse, The product of two inverse matrices is always the identity) https://www.mathbootcamps.com/the-identity-matrix-and-its-properties/

    

   Identitātes matricas var izmantot, lai pārbaudītu vai Inverse ir pareizi izrēķināti

   $$\begin{array}{}\text{(4)}& W^{-1}\cdot W=I\end{array}$$

    

    

7. Pārveidot 3d vektorus uz 2d vektoriem un otrādi tikai izmantojot identitātes matricas, dot product un saskaitīšanu

8. Implementēt kodu kopā, lai kuģis varētu lidot

9. translation matrix

10. combined matrix Rotate, then translate

11. Riņķa līnijas algoritma piemērs:

12. gravity forces

    1. Physics $F=\frac{G(m_1\cdot m_2)}{d^2}$$F = \frac{G (m_1 \cdot m_2)}{d^2}$

    2. Distance $d=\sqrt{(po{s}_{planet}-po{s}_{player}{)}^2}$$d = \sqrt{(pos_{planet}- pos_{player})^2}$

    3. Game physics $F=\frac{C_{planet}}{d^2}$$F = \frac{C_{planet}}{d^2}$

13. l2 norm

14. Labojot mājasdarbu pārliecināties, ka studenti izmanto jaunāko template, ka netiek iesniegti darbi no iepriekšējiem gadiem ar pinīgi atšķirīgu template

https://www.youtube.com/watch?v=_TKiRvGfw3Q